This tutorial is created by Rosbotics Ambassador 017 Jose
Rosbotics Ambassador Program ((https://www.theconstruct.ai/rosbotics-ambassador/)
Lo que vamos a aprender
- Subscribirse al tópico /odom y asi conocer la posición estimada del robot.
- Publicar en el tópico /cmd_vel, para así mover al robot de acuerdo con la posición estimada.
Lista de recursos usados en esta publicación
- Usa este rosject: https://app.theconstructsim.com/l/5fc977f5/
- The Construct: https://app.theconstructsim.com/
- Cursos ROS: ROS2 Basics in 5 Days (Python): https://app.theconstructsim.com/courses/132
Resumen
ROS (Robot Operating System) se está convirtiendo en el “framework” estándar para programar robots. En este tutorial emplearemos los conceptos de tópicos y nodos para mover el robot “Turtlebot3” hacia múltiples posiciones deseadas. Hacemos uso de los mensajes del tópico /odom para conocer la posición estimada del robot y publicar en el tópico /cmd_vel para mover el robot a las posiciones deseadas. Todo esto es simulado en un mundo de Gazebo. Ten encuesta que se usará ROS2 Humble para este tutorial.
PASO 1: Abriendo el rosject
Para seguir este tutorial, necesitamos tener instalado ROS2 HUMBLE en nuestro sistema, y lo ideal sería tener un ros2_ws (Espacio de Trabajo ROS2). Para facilitarte la vida, ya hemos preparado un rosject para eso: https://app.theconstructsim.com/l/5fc977f5/.
Simplemente copiando el rosject (haciendo clic en el enlace de arriba), tendrás una configuración ya preparada para ti.
Después de haber copiado el rosject a tu propia área de trabajo, deberías ver el botón RUN. Haz clic en ese botón para lanzar el rosject (abajo tienes un ejemplo de rosject).
Tras pulsar el botón RUN, deberías tener cargado el rosject. Ahora, pasemos a la siguiente sección para ponernos manos a la obra.
PASO 2: Desarrollo del paquete
El robot a usar es el Turtlebot3.
Estrategia de control
El Turtlebot3 se moverá por una serie de posiciones en un orden específico, es decir, se moverá de su posición inicial a la 1ra posición deseada, una vez alcanzada, se moverá a la 2da posición y así sucesivamente. Para lograr esto, necesitamos de una estrategia.
Tengamos en cuenta que el robot conocerá las posiciones que debe alcanzar y su posición actual estimada gracias al tópico /odom, del cual aprovecharemos la posición en X, posición Y, y la rotación en Z.
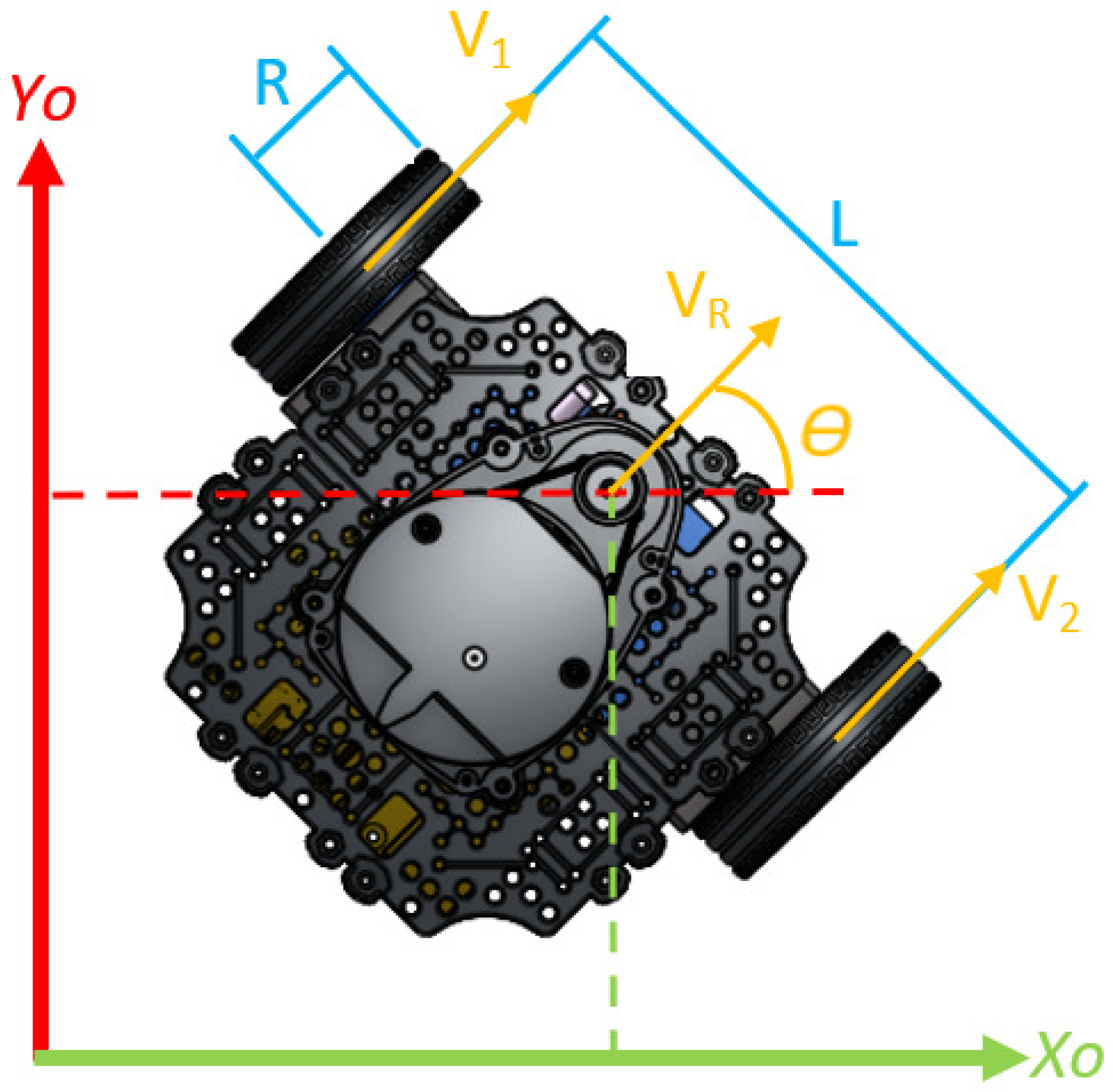
Con ello, para alcanzar cada posición el Turtlebot3 realizará 2 movimientos: Primero, girar hasta que quede mirando a la posición deseada; Segundo, avanzar de manera recta hasta llegar a la posición.

Adicionalmente, debemos tener en cuenta el robot no se moverá en una línea recta de manera perfecta, por lo que se requiere compensar esa desviación conforme avanza. Esto se puede realizar añadiendo una velocidad angular cuando la orientación cambie demasiado.
Creación del paquete
Primero creamos un paquete en python para realizar un nodo-publicador-subscriptor que mueva al Turtlebot3 de la forma deseada. Necesitamos añadir las dependencias necesarias. Para ello ejecutamos en un terminal lo siguiente:
cd ~/ros2_ws/src
ros2 pkg create --build-type ament_python turtlebot3_tutorial --dependencies std_msgs geometry_msgs
Creación del nodo
Creamos el archivo que contendrá el nodo.
cd ~/ros2_ws/src/turtlebot3_tutorial/turtlebot3_tutorial
touch turtlebot3_node.py
Copiamos el siguiente código dentro del archivo.
import rclpy
from rclpy.node import Node
from geometry_msgs.msg import Twist
from nav_msgs.msg import Odometry
from rclpy.qos import ReliabilityPolicy, QoSProfile
import numpy as np
import math
class Robot(Node):
def __init__(self):
super().__init__('turtlebot3_node')
# Posiciones estimadas
self.pos_x = 0
self.pos_y = 0
self.roll = 0
self.pitch = 0
self.yaw = 0
# Velocidad de desplazamiento
self.vel_linear_x = 0.2
self.vel_angular_z = 0.4
# Máximo error
self.linear_error = 0.08
self.angular_error = 0.05
# Posiciones deseadas
self.posiciones = [[1,1], [0,2], [0, 0]]
self.index = 0
self.pos_x_d, self.pos_y_d = self.posiciones[self.index]
self.angulo_d = 0
# Fase
self.fase = 1
# Subscriptor
self.subscriber = self.create_subscription(
Odometry,
'/odom',
self.listener_callback,
QoSProfile(depth=10, reliability=ReliabilityPolicy.RELIABLE))
# Publicador
self.publisher_ = self.create_publisher(Twist, 'cmd_vel', 10)
self.vel = Twist()
timer_period = 0.1
self.timer = self.create_timer(timer_period, self.timer_callback)
def timer_callback(self):
if (self.index < len(self.posiciones)):
self.pos_x_d, self.pos_y_d = self.posiciones[self.index]
if (self.fase == 1):
# Calcular ángulo de rotación
self.angulo_d = math.atan2(self.pos_y_d - self.pos_y, self.pos_x_d - self.pos_x)
if ( abs(self.yaw - self.angulo_d) > self.angular_error ):
self.vel.linear.x = 0.0
self.vel.angular.z = self.vel_angular_z if self.yaw < self.angulo_d else -self.vel_angular_z
else:
self.vel.linear.x = 0.0
self.vel.angular.z = 0.0
self.fase += 1
if (self.fase == 2):
if ( math.sqrt((self.pos_x - self.pos_x_d)**2 + (self.pos_y - self.pos_y_d)**2) > self.linear_error ):
self.vel.linear.x = self.vel_linear_x
if ( abs(self.yaw - self.angulo_d) > self.angular_error):
self.vel.angular.z = self.vel_angular_z if self.yaw < self.angulo_d else -self.vel_angular_z
else:
self.vel.angular.z = 0.0
else:
self.vel.linear.x = 0.0
self.vel.angular.z = 0.0
self.fase = 1
# Siguiente posición deseada
self.index += 1
self.publisher_.publish(self.vel)
def listener_callback(self, msg):
self.pos_x = msg.pose.pose.position.x
self.pos_y = msg.pose.pose.position.y
quaternion = [msg.pose.pose.orientation.x,
msg.pose.pose.orientation.y,
msg.pose.pose.orientation.z,
msg.pose.pose.orientation.w]
self.roll, self.pitch, self.yaw = self.euler_from_quaternion(quaternion)
self.get_logger().info('Pos_x: "%f"' % self.pos_x)
self.get_logger().info('Pos_y: "%f"' % self.pos_y)
self.get_logger().info('Ori_z: "%f"' % self.yaw)
self.get_logger().info('-------------------------')
def euler_from_quaternion(self, quaternion):
"""
Converts quaternion (w in last place) to euler roll, pitch, yaw
quaternion = [x, y, z, w]
Below should be replaced when porting for ROS2 Python tf_conversions is done.
"""
x = quaternion[0]
y = quaternion[1]
z = quaternion[2]
w = quaternion[3]
sinr_cosp = 2 * (w * x + y * z)
cosr_cosp = 1 - 2 * (x * x + y * y)
roll = np.arctan2(sinr_cosp, cosr_cosp)
sinp = 2 * (w * y - z * x)
pitch = np.arcsin(sinp)
siny_cosp = 2 * (w * z + x * y)
cosy_cosp = 1 - 2 * (y * y + z * z)
yaw = np.arctan2(siny_cosp, cosy_cosp)
return roll, pitch, yaw
def main(args=None):
# initialize the ROS communication
rclpy.init(args=args)
robot = Robot()
rclpy.spin(robot)
robot.destroy_node()
rclpy.shutdown()
if __name__ == '__main__':
main()
Repasemos las partes más importantes del código:
- Aquí iniciamos el subscriptor del tópico /odom y el publicador al tópico /cmd_vel
# Subscriptor
self.subscriber = self.create_subscription(
Odometry,
'/odom',
self.listener_callback,
QoSProfile(depth=10, reliability=ReliabilityPolicy.RELIABLE))
# Publicador
self.publisher_ = self.create_publisher(Twist, 'cmd_vel', 10)
self.vel = Twist()
timer_period = 0.1
self.timer = self.create_timer(timer_period, self.timer_callback)
- En el método listener_callback recibimos las posiciones estimadas del robot y las acondicionamos para emplearlas en la lógica de control.
def listener_callback(self, msg):
self.pos_x = msg.pose.pose.position.x
self.pos_y = msg.pose.pose.position.y
quaternion = [msg.pose.pose.orientation.x,
msg.pose.pose.orientation.y,
msg.pose.pose.orientation.z,
msg.pose.pose.orientation.w]
self.roll, self.pitch, self.yaw = self.euler_from_quaternion(quaternion)
self.get_logger().info('Pos_x: "%f"' % self.pos_x)
self.get_logger().info('Pos_y: "%f"' % self.pos_y)
self.get_logger().info('Ori_z: "%f"' % self.yaw)
self.get_logger().info('-------------------------')
- Debido a que en el tópico /odom la orientación es expresada en cuaterniones, el método euler_from_quaternion es necesario para convertir la orientación del robot de cuaterniones a la notación roll-pitch-yaw. Esto nos permite obtener la rotación del robot alrededor del eje z (yaw).
def euler_from_quaternion(self, quaternion):
"""
Converts quaternion (w in last place) to euler roll, pitch, yaw
quaternion = [x, y, z, w]
Below should be replaced when porting for ROS2 Python tf_conversions is done.
"""
x = quaternion[0]
y = quaternion[1]
z = quaternion[2]
w = quaternion[3]
sinr_cosp = 2 * (w * x + y * z)
cosr_cosp = 1 - 2 * (x * x + y * y)
roll = np.arctan2(sinr_cosp, cosr_cosp)
sinp = 2 * (w * y - z * x)
pitch = np.arcsin(sinp)
siny_cosp = 2 * (w * z + x * y)
cosy_cosp = 1 - 2 * (y * y + z * z)
yaw = np.arctan2(siny_cosp, cosy_cosp)
return roll, pitch, yaw
- Este es el método definido en el timer y contiene la estrategia de control explicada anteriormente. Se ejecuta cada 0.1s y actualiza la velocidad del robot de acuerdo con la posición estimada.
def timer_callback(self):
if (self.index < len(self.posiciones)):
self.pos_x_d, self.pos_y_d = self.posiciones[self.index]
if (self.fase == 1):
# Calcular ángulo de rotación
self.angulo_d = math.atan2(self.pos_y_d - self.pos_y, self.pos_x_d - self.pos_x)
if ( abs(self.yaw - self.angulo_d) > self.angular_error ):
self.vel.linear.x = 0.0
self.vel.angular.z = self.vel_angular_z if self.yaw < self.angulo_d else -self.vel_angular_z
else:
self.vel.linear.x = 0.0
self.vel.angular.z = 0.0
self.fase += 1
if (self.fase == 2):
if ( math.sqrt((self.pos_x - self.pos_x_d)**2 + (self.pos_y - self.pos_y_d)**2) > self.linear_error ):
self.vel.linear.x = self.vel_linear_x
if ( abs(self.yaw - self.angulo_d) > self.angular_error):
self.vel.angular.z = self.vel_angular_z if self.yaw < self.angulo_d else -self.vel_angular_z
else:
self.vel.angular.z = 0.0
else:
self.vel.linear.x = 0.0
self.vel.angular.z = 0.0
self.fase = 1
# Siguiente posición deseada
self.index += 1
self.publisher_.publish(self.vel)
Creación del launch
Una vez que el nodo esta listo creamos el archivo launch con lo siguiente:
cd ~/ros2_ws/src/turtlebot3_tutorial
mkdir launch
cd launch
touch turtlebot3_launch.launch.py
chmod +x turtlebot3_launch.launch.py
Copiamos el siguiente código dentro del archivo que acabamos de crear:
from launch import LaunchDescription
from launch_ros.actions import Node
def generate_launch_description():
return LaunchDescription([
Node(
package='turtlebot3_tutorial',
executable='turtlebot3_node',
output='screen'),
])
Una vez hecho lo anterior, editamos el archivo setup.py para añadir nuestro nodo.
from setuptools import setup
import os # <-- Añadir
from glob import glob # <-- Añadir
package_name = 'turtlebot3_tutorial'
setup(
name=package_name,
version='0.0.0',
packages=[package_name],
data_files=[
('share/ament_index/resource_index/packages',
['resource/' + package_name]),
('share/' + package_name, ['package.xml']),
(os.path.join('share', package_name), glob('launch/*.launch.py')) # <-- Añadir
],
install_requires=['setuptools'],
zip_safe=True,
maintainer='user',
maintainer_email='user@todo.todo',
description='TODO: Package description',
license='TODO: License declaration',
tests_require=['pytest'],
entry_points={
'console_scripts': [
'turtlebot3_node = turtlebot3_tutorial.turtlebot3_node:main' # <-- Añadir de acuerdo al nombre de tu paquete y script
],
},
)
Compilación del paquete
Por último, compilamos el paquete antes de ejecutar la simulación.
cd ~/ros2_ws
pip install setuptools==58.2.0
colcon build --packages-select turtlebot3_tutorial
source install/setup.bash
PASO 3: Simulando en Gazebo
Finalmente simularemos el comportamiento en gazebo, para ello primero iniciamos la simulación del Turtlebot3, cuyo paquete ya esta en este rosject. Esta se puede obtener desde este link.
export TURTLEBOT3_MODEL=waffle
ros2 launch turtlebot3_gazebo empty_world.launch.py
Una vez que se inicio la simulación, ya podemos iniciar el nodo que creamos.
ros2 launch turtlebot3_tutorial turtlebot3_launch.launch.py
Y listo! Ya podemos observar al robot moviendose por todas las posiciones deseadas en el orden especificado.






0 Comments