About

In this tutorial, we are going to answer a question found at ROS answers – How to convert quaternions to Euler angles?

We’ll explain this with the following example in ROS Development Studio (ROSDS), where you can easily follow the steps and understand how to use the conversion from quaternions provided by an Odometry message to Euler angles (Roll, Pitch, and Yaw).

---

Step1. Create a Project in RDS

If you haven’t had an account yet, register here for free. 

We’ll use a simulation we built previously, you can find some information here and build it in 5 mins with RDS.

Launch the Turtlebot 3 empty world simulation with the following command

$ roslaunch turtlebot3_gazebo turtlebot3_empty_world.launch

---

Step2. Create Package

We then create another package called my_quaternion_pkg for this example  under the ~/catkin_ws/src using

$ catkin_create_pkg my_quaternion_pkg rospy

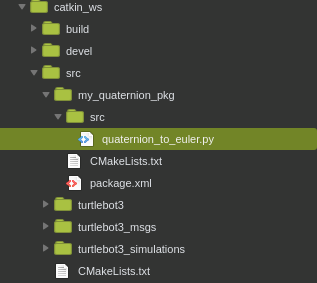
Create a quaternion_to_euler.py file under my_quaternion_pkg. Now the source tree may look like the following picture

---

Step3. Transform Quaternion to Euler

As our first attempt, copy the following code into the quaternion_to_euler.py file

#!/usr/bin/env python
import rospy
from nav_msgs.msg import Odometry

def get_rotation (msg):
    print msg.pose.pose.orientation

rospy.init_node('my_quaternion_to_euler')

sub = rospy.Subscriber ('/odom', Odometry, get_rotation)

r = rospy.Rate(1)
while not rospy.is_shutdown():
    r.sleep()

To run the file, simply type

$ rosrun my_quaternion_pkg quaternion_to_euler.py

Now you can see the code prints the odometry message in quaternion format. Now, we’d like to transform it to Euler angles. We use the euler_from_quaternion function provided by tf.transformations, you can find more detail here

#!/usr/bin/env python
import rospy
from nav_msgs.msg import Odometry
from tf.transformations import euler_from_quaternion, quaternion_from_euler

def get_rotation (msg):
    global roll, pitch, yaw
    orientation_q = msg.pose.pose.orientation
    orientation_list = [orientation_q.x, orientation_q.y, orientation_q.z, orientation_q.w]
    (roll, pitch, yaw) = euler_from_quaternion (orientation_list)
    print yaw

rospy.init_node('my_quaternion_to_euler')

sub = rospy.Subscriber ('/odom', Odometry, get_rotation)

r = rospy.Rate(1)
while not rospy.is_shutdown():
    r.sleep()

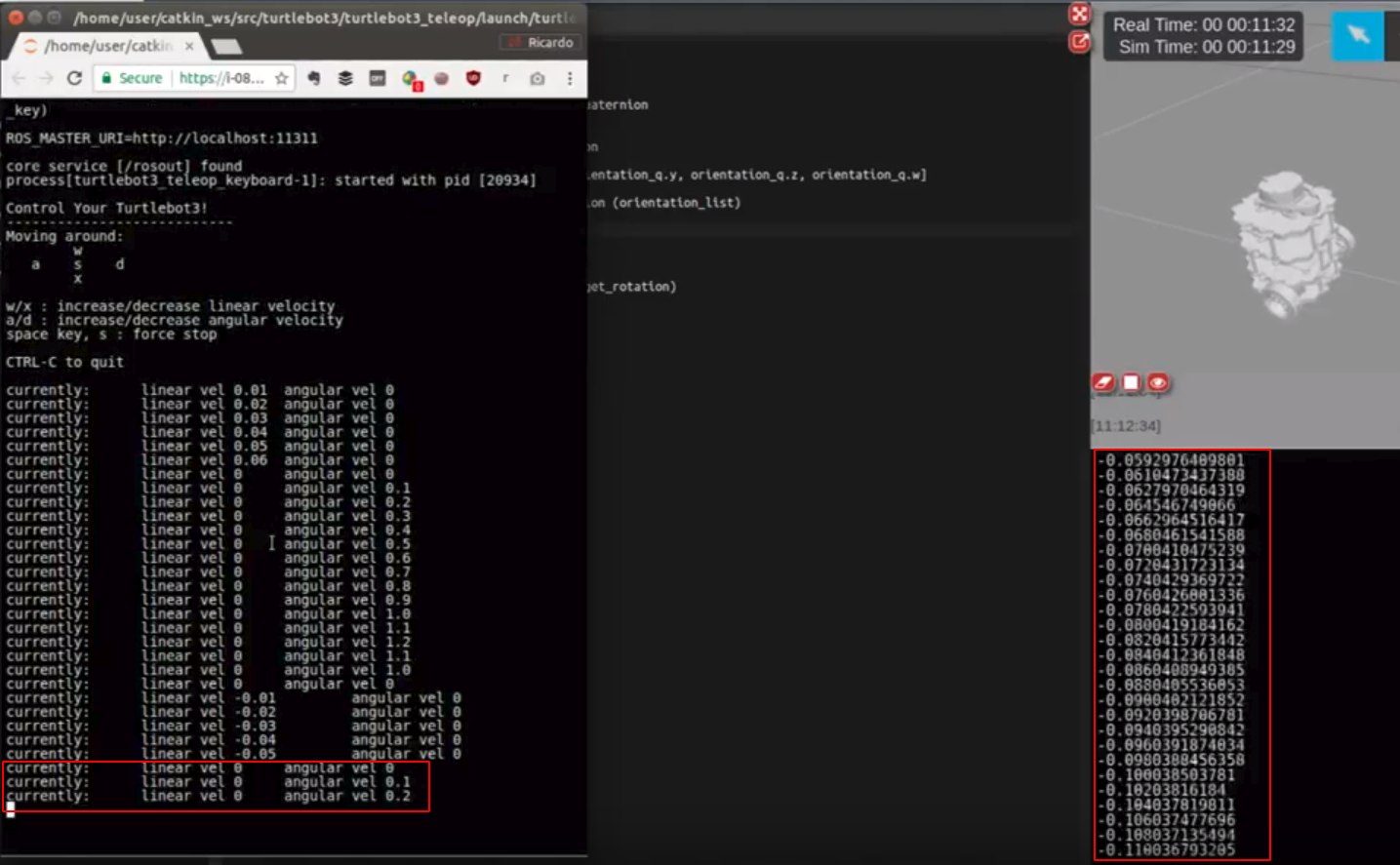
We only print yaw values here. You can check it by typing the following command to control the Turtlebot.

$ roslaunch turtlebot3_teleop turtlebot3_teleop_key.launch

If you turn the robot, you’ll see the yaw angle change accordingly.

---

Step4. Transform Euler to Quaternion

Similarly, we can use the quaternion_from_euler function provided by tf.transformations to transform the Euler back to the quaternion with the following code.

#!/usr/bin/env python
import rospy
from nav_msgs.msg import Odometry
from tf.transformations import euler_from_quaternion, quaternion_from_euler

roll = pitch = yaw = 0.0

def get_rotation (msg):
    global roll, pitch, yaw
    orientation_q = msg.pose.pose.orientation
    orientation_list = [orientation_q.x, orientation_q.y, orientation_q.z, orientation_q.w]
    (roll, pitch, yaw) = euler_from_quaternion (orientation_list)
    print yaw

rospy.init_node('my_quaternion_to_euler')

sub = rospy.Subscriber ('/odom', Odometry, get_rotation)

r = rospy.Rate(1)
while not rospy.is_shutdown():
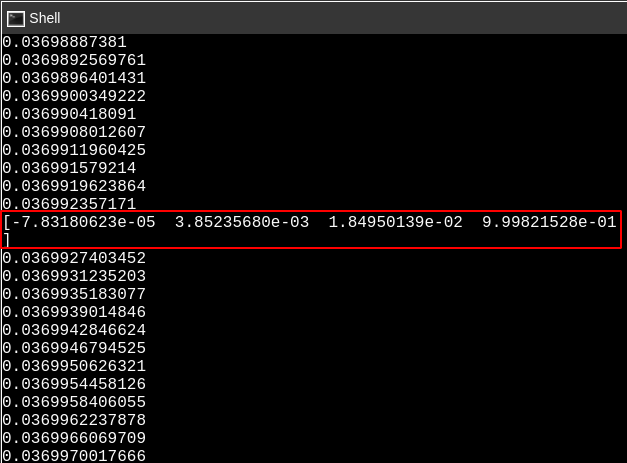
    quat = quaternion_from_euler (roll, pitch,yaw)
    print quat
    r.sleep()

The quaternion will print every 1 second since we specified the rate for 1 Hz and the odometry topic is published in 100 Hz.

---

Takeaway Today:

You can transform between Euler and quaternion using the quaternion_from_euler and euler_from_quaternion function provided by the tf.transform.

 

Edit by Tony Huang

Related Courses